SUSTRACCIÓN ARITMÉTICA PROBLEMAS RESUELTOS
¿Qué es la sustracción ?
Es una operación inversa a la adición , tal que dados dos números llamados minuendo y sustraendo hace corresponder un tercer número llamado diferencia, tal que sumando con el sustraendo de como resultado el minuendo.
- CLIC AQUÍ Ver ADICIÓN ARITMÉTICA TEORÍA Y EJERCICIOS RESUELTOS PDF
- Ver SUMA EN OTRAS BASES
- Ver SUSTRACCIÓN ARITMÉTICA
- Ver RESTA EN OTRAS BASES
- Ver COMPLEMENTO ARITMÉTICO
- Ver MULTIPLICACIÓN ARITMÉTICA
- Ver MULTIPLICACIÓN EN OTRAS BASES
- Ver DIVISIÓN ARITMÉTICA
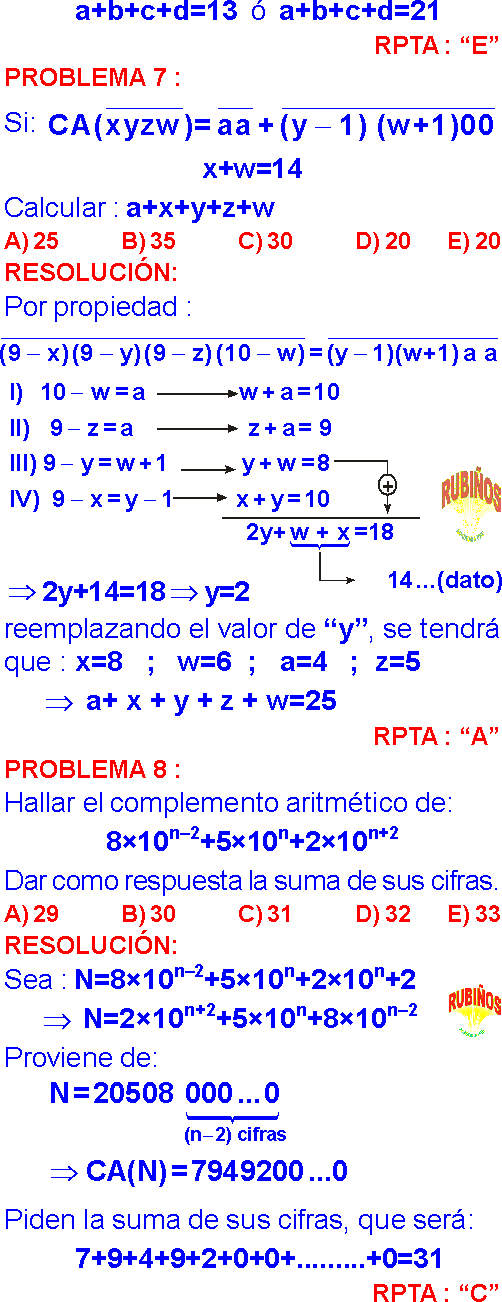
EJERCICIO 1 :
Se tiene un número de 4 cifras significativas que sumadas dan 32, entonces la suma de cifras de su C.A. es:
Rpta. : "5"
EJERCICIO 2 :
La suma de los tres términos de una resta es 1480. Si el sustraendo es el C.A. del minuendo, calcular el cuádruplo de la tercera parte de la diferencia.
Rpta. : "640"