ESTADÍSTICA EXPLICACIONES BÁSICAS PARA PRINCIPANTES PDF
CONCEPTO DE ESTADÍSTICA
Es la ciencia que proporciona un conjunto de informaciones, métodos y procedimientos para la recolección, clasificación, análisis e interpretación de los datos para tomar decisiones.
- CLIC AQUÍ Ver ESTADÍSTICA TEORÍA Y EJERCICIOS RESUELTOS
- Ver ESTADÍSTICA NIVEL BÁSICO
- Ver ESTADÍSTICA FULL PROBLEMAS RESUELTOS
- Ver PRACTICA DE ESTADÍSTICA CON RESPUESTAS
- Ver VARIABLES ESTADÍSTICAS
- Ver TABLAS DE DISTRIBUCIÓN DE FRECUENCIAS
- Ver TABLAS Y GRÁFICOS ESTADÍSTICOS
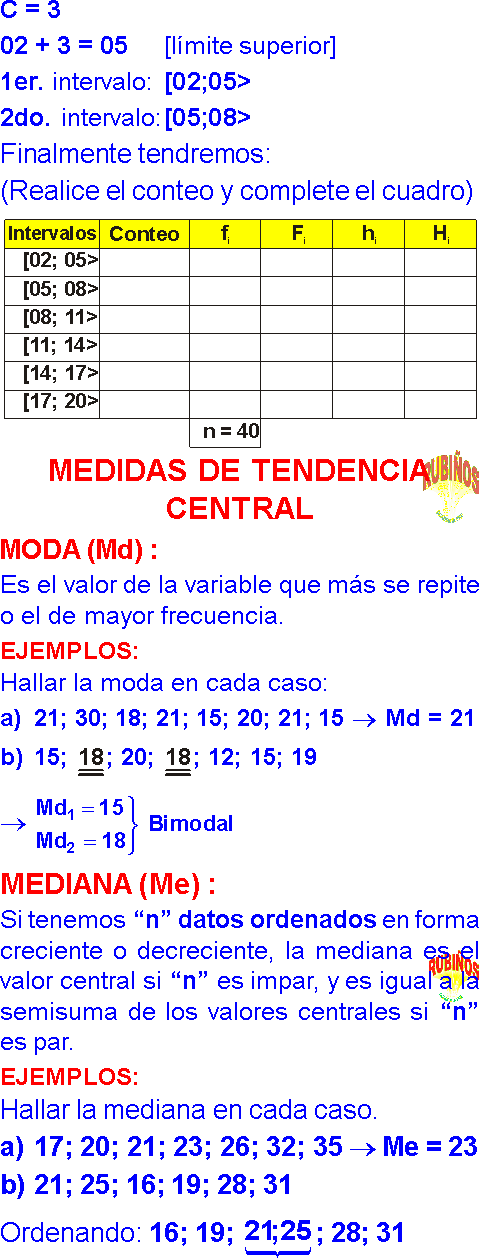
- Ver MEDIDAS DE TENDENCIA CENTRAL
- Ver MEDIDAS DE DISPERSIÓN
- Ver INTERPRETACIÓN DE GRÁFICAS ESTADÍSTICAS
La investigación estadística es fundamentalmente de tipo descriptiva.
Se preocupa de la confiabilidad, validez y significación de los datos de las muestras, así como de los métodos y técnicas de recolección y análisis estadístico.