COMPARACIÓN DE FRACCIONES EJEMPLOS RESUELTOS-RELACIÓN DE ORDEN DE MAYOR A MENOR

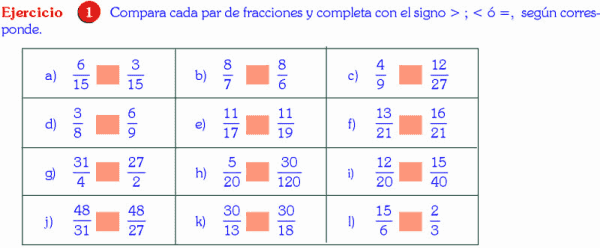
Comparación de fracciones homogéneas Dos o más fracciones son homogéneas si tienen el mismo denominador. Al comparar dos fracciones homogéneas, es mayor la que tiene mayor numerador. Ejemplos: I. Comparación de fracciones heterogéneas Dos o más fracciones son heterogéneas si sus denominadores no son iguales. Para comparar dos fracciones heterogéneas se siguen los siguientes pasos: 1° Si las fracciones no son irreductibles se las simplifica hasta hacerlas irreductibles 2° Se reducen las fracciones a su mínimo común denominador 3° Se comparan las fracciones homogéneas halladas. Ejemplo 1. ¿Qué fracción es mayor ó ? Resolución: 1° Simplificamos las fracciones: y 2° Se reducen las fracciones 2/5 y 2/3 a su mínimo común denominador. 3° Comparamos las fracciones homogéneas halladas, es decir: y Luego: Þ La manera práctica de comparar dos fracciones es aplicando “Productos Cruzados”, veamos: ¿Qué fracción es mayor? Resolución: Þ 12 ´ 24 < 16 ´ 30 Þ 1 Compara cada par de fracciones y escribe entre ellos, según corresponda, uno de los símbolos >, <, =. a) g) m) b) h) n) c) i) o) d) j) p) e) k) q) f) l) r) 2 Coloca en cada paréntesis “F” en cada caso que sea falso y “V” en cada caso que sea verdadero. Ordena de mayor a menor las siguientes fracciones que se presentan en cada caso. a) Resolución: * Comparamos con aplicando el “Producto cruzado” Þ (a) * Comparamos 3/5 con 2/3 aplicando el “Producto cruzado” Þ Al decir que es menor que , es lo mismo decir que es mayor que , entonces: (b) Luego de las expresiones (b) y (a), obtenemos: Þ Nota: Estas fracciones están ordenadas de mayor a menor. A) Si se tiene un grupo de fracciones homogéneas , será mayor aquella que tenga mayor numerador. Ejemplo: Sean las fracciones: Ordenando de menor a mayor. B) Si se tiene un grupo de fracciones de igual numerador, es mayor la fracción que posee menor denominador. Ejemplo: Sean las fracciones: Ordenando de menor a mayor. Relación de orden Una manera práctica de comparar dos fracciones es utilizando la regla de los productos cruzados. Ejemplo: ¿Cuál de las siguientes fracciones es mayor? Hacemos: y como: 35 > 27 entonces: Para comparar más de 2 fracciones se puede comparar de dos en dos. Transformando las fracciones a denominador común Ordenar las siguientes fracciones de menor a mayor: Paso 1: Hallamos el m.c.m. de los denominadores: m.c.m. (9; 5; 12) = 180 Paso 2: Paso 3: Ordenando de acuerdo a los numeradores: