OPERACIONES CON CONJUNTOS EJEMPLOS
- CLIC AQUÍ Ver CONJUNTOS TEORÍA Y EJERCICIOS RESUELTOS
- Ver DETERMINACIÓN DE CONJUNTOS
- Ver RELACIONES ENTRE CONJUNTOS
- Ver CLASES DE CONJUNTOS
- Ver OPERACIONES CON CONJUNTOS
- Ver DIAGRAMAS DE VENN EN 2 CONJUNTOS EJERCICIOS RESUELTOS
- Ver DIAGRAMAS DE VENN EN 3 CONJUNTOS
- Ver DIAGRAMAS DE CARROL
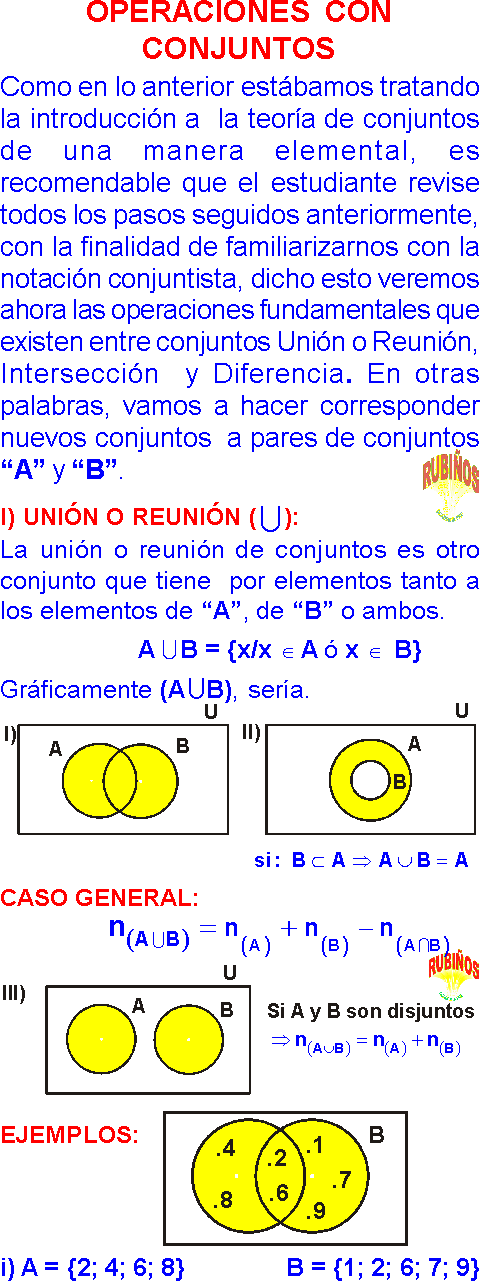
Como en lo anterior estábamos tratando la introducción a la teoría de conjuntos de una manera elemental, es recomendable que el estudiante revise todos los pasos seguidos anteriormente, con la finalidad de familiarizarnos con la notación conjuntista, dicho esto veremos ahora las operaciones fundamentales que existen entre conjuntos Unión o Reunión, Intersección y Diferencia. En otras palabras, vamos a hacer corresponder nuevos conjuntos a pares de conjuntos “A” y “B”. I) Unión o reunión (): La unión o reunión de conjuntos es otro conjunto que tiene por elementos tanto a los elementos de “A”, de “B” o ambos. Gráficamente (AB), sería. Caso general: Ejemplos: II) La Intersección () : La intersección de 2 conjuntos A y B es otro conjunto que tiene por elementos, a los elementos al de A y de B a la vez. Gráficamente (AB), sería: EJEMPLOS : III) La Diferencia (–) : La diferencia de 2 conjuntos A y B es otro conjunto que tiene por elementos a los elementos que pertenecen al conjunto A pero no al conjunto B. A – B = {x/xÎA y x B} Gráficamente (A – B), sería: Ejemplos : i) A = {2; 4; 6; 8} B = {1; 2; 6; 7; 9} A – B = {4; 8} ii) C = {2; 3; 4; 5; 6;} D = {3; 5; 6} C – D = {2; 4} iii) E = {1; 3; 5; 7} F = {2; 4; 6; 8} E – F = {1; 3; 5; 7} IV) La Diferencia Simétrica ( d ) : La diferencia simétrica de 2 conjuntos A y B es otro conjunto que tiene por elementos a los elementos de la reunión de las dos diferencias A – B y B – A ,es decir: A d B = (A – B)(B – A) Gráficamente ( A d B ), sería: Ejemplos : i) A = {2; 4; 6; 8} B = {1; 2; 6; 7; 9} A d B = {1; 4; 7; 8; 9} ii) C = {2; 3; 4; 5; 6} D = {3; 5; 6} C d D = {2; 4} iii) E = {1; 3; 5; 7} F = {2; 4; 6; 8} E d F = {1; 2; 3; 4; 5; 6; 7; 8; 9} COMPLEMENTO DE (Ac) El complemento de un conjunto A es el conjunto formado por los elementos que pertenecen al conjunto universal “U” pero no al Conjunto “A” Notación: A´ ó Ac Se lee: complemento de A: Ejemplo: Sean los conjuntos: R = {1; 4; 6} P = {2; 4; 6} además: U={1; 2; 3; 4; 5; 6; 7} Entonces: R’ = {2; 3; 5; 7} P’ = {1; 3; 5; 7} Gráficamente: En las operaciones: unión, intersección diferencia simétrica se cumple la propiedad conmutativa, es decir: En la diferencia no se cumple, es decir: INTERPRETACION DE REGIONES I) PARA 2 CONJUNTOS